Cross Entropy Loss¶

In [1]:
from IPython.display import display, HTML
display(HTML("<style>.container { width:85% !important; }</style>"))

1. Measuring performance of a model¶

In [26]:
import torch
import torch.nn.functional as F
from torch import tensor

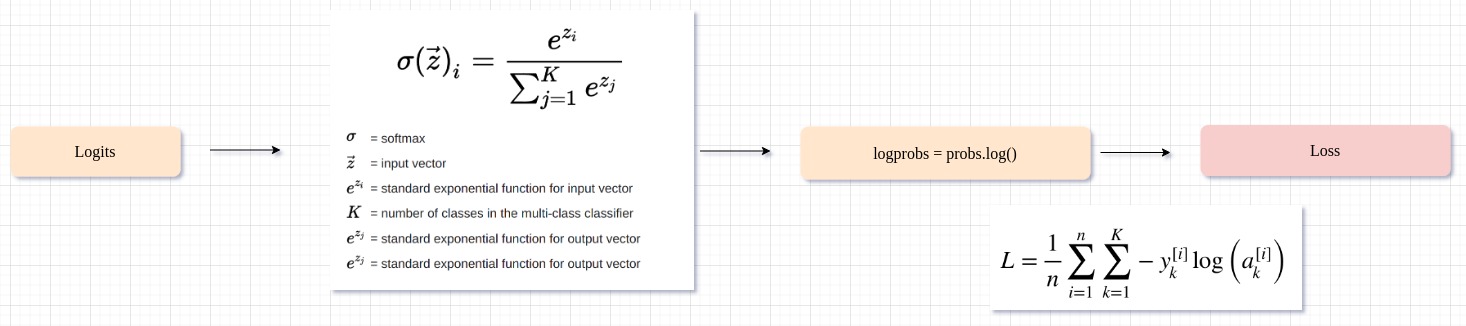
./images/classification-loss.jpg

In the The spelled-out intro to language modeling: building makemore lecture, Karpathy says that

  • When you look at the literature into maximum likelihood estimation and statistical modeling and so on, you'll see that what's typically used here is something called the likelihood and the likelihood is the product of all of these probabilities
  • So the product of all these probabilities is the likelihood, and it's really telling us about the probability of the entire data set assigned by the model that we've trained and that is a measure of quality
  • So the product of these should be as high as possible when you are training the model and when you have a good model Your product of these probabilities should be very high.
  • Now because the product of these probabilities is an unwieldy thing to work with, you can see that all of them are between zero and one

So your product of these probabilities will be a very tiny number. So for convenience, what people work with usually is not the likelihood, but they work with what's called the log likelihood.

But, why do we need Negative log likelyhoold? I asked Claude for help. This is what I got:

The negative sign in the cross-entropy loss formula serves an important purpose.

  1. Likelihood and probability:

The likelihood of an event is typically expressed as a probability between 0 and 1. For example, if a model predicts an event with 80% confidence, the likelihood is 0.8.

  1. Properties of logarithms:

The logarithm of a number between 0 and 1 is always negative. For instance: 

log(0.8) ≈ -0.223
log(0.5) ≈ -0.693
log(0.1) ≈ -2.303
  1. Goal of loss functions:

In machine learning, we typically want to minimize the loss function. Lower loss indicates better model performance.

  1. Inverting the scale:

By adding the negative sign, we invert the scale of the logarithm. This accomplishes two things: a. It makes the loss positive, which is more intuitive. b. It aligns the loss with our goal of minimization.

Here's how it works:

  • For high likelihood predictions (close to 1), the negative log likelihood will be a small positive number.
  • For low likelihood predictions (close to 0), the negative log likelihood will be a large positive number.

This way, minimizing the loss corresponds to maximizing the likelihood of correct predictions.

To illustrate:

  • If prediction = 0.9 (good), -log(0.9) ≈ 0.105 (small loss)
  • If prediction = 0.1 (poor), -log(0.1) ≈ 2.303 (large loss)

Without the negative sign, we'd have to maximize the loss to improve the model, which is counterintuitive.

In [27]:
import numpy as np
import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(8, 6))
x = np.linspace(0.01, 1, 1000)
y = np.log(x)
plt.plot(x, y)

# Set labels and title
plt.xlabel('x')
plt.ylabel('log(x)')
plt.title('For x between 0 and 1, log(x) is negative')
plt.grid(True, linestyle='--', alpha=0.7)
plt.xlim(0, 1)
plt.axvline(x=0, color='r', linestyle='--', label='(x=0)')
plt.legend()
plt.show()
No description has been provided for this image

2. Calculating loss manually¶

In [28]:
# We have 4 samples and 3 classes
# "logits" is the output of the model before applying softmax
logits = torch.tensor([
    [1.5, 0.1, -0.4],
    [0.5, 0.7, 2.1],
    [-2.1, 1.1, 0.8],
    [1.1, 2.5, -1.2]
])
In [29]:
# Softmax normalizes the logits
probs = torch.softmax(logits, dim=1)
probs
Out[29]:
tensor([[0.7162, 0.1766, 0.1071],
        [0.1394, 0.1702, 0.6904],
        [0.0229, 0.5613, 0.4158],
        [0.1940, 0.7866, 0.0194]])
In [30]:
# Sum of the row elements is 1
probs.sum(dim=1)
Out[30]:
tensor([1.0000, 1.0000, 1.0000, 1.0000])

True Labels¶

In [31]:
y = torch.tensor([0, 2, 2, 1])
y_onehot = F.one_hot(y, num_classes=3)

print(y_onehot)

tensor([[1, 0, 0],
        [0, 0, 1],
        [0, 0, 1],
        [0, 1, 0]])

Cross Entropy Loss¶

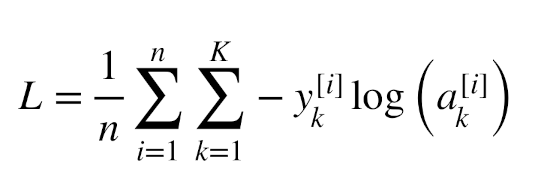
./images/cross-entropy-loss.png

In [32]:
### Training example #1
probs[0], y_onehot[0]
Out[32]:
(tensor([0.7162, 0.1766, 0.1071]), tensor([1, 0, 0]))
In [33]:
(-1 * torch.log(tensor(0.7162))) + (-0 * torch.log(tensor(0.1766))) + (-0 * torch.log(tensor(0.1071)))
Out[33]:
tensor(0.3338)
In [34]:
### Training example #2
probs[1], y_onehot[1]
Out[34]:
(tensor([0.1394, 0.1702, 0.6904]), tensor([0, 0, 1]))
In [35]:
0 + 0 + (-1 * torch.log(tensor(0.6904)))
Out[35]:
tensor(0.3705)
In [36]:
### Training example #3
probs[2], y_onehot[2]
Out[36]:
(tensor([0.0229, 0.5613, 0.4158]), tensor([0, 0, 1]))
In [37]:
0 + 0 + (-1 * torch.log(tensor(0.4158)))
Out[37]:
tensor(0.8776)
In [38]:
### Training example #4
probs[3], y_onehot[3]
Out[38]:
(tensor([0.1940, 0.7866, 0.0194]), tensor([0, 1, 0]))
In [39]:
0 + (-1 * torch.log(tensor(0.7866))) + 0
Out[39]:
tensor(0.2400)
In [40]:
# Cross Entropy Loss
L = (0.3338 + 0.3705 + 0.8776 + 0.2400) / 4
print(L)

0.455475

2. Calculating loss using Python¶

In [41]:
def loss_using_python():
    probs = torch.softmax(logits, dim=1)
    n, _ = probs.shape
    no_classes = 3
    loss = 0

    for i in range(n):
        true_label_index = y[i].item()
        one_hot = (F.one_hot(torch.tensor(true_label_index), no_classes))

        one_hot_sum = 0

        for k in range(no_classes):
            neg_log_likelihood = -1 * torch.log(probs[i][k])
            one_hot_sum += one_hot[k] * neg_log_likelihood

        loss += one_hot_sum

    print(f"Loss: {(loss / n)}")


loss_using_python()

Loss: 0.45545268058776855

3. Manually calculating in PyTorch¶

In [42]:
def manual_cross_entropy(logits, y):
    """
    logits: Is the output of the model before applying softmax
    y: True labels
    """
    probs = F.softmax(logits, dim=1)
    y_onehot = F.one_hot(y)
    train_loss = -torch.sum(y_onehot * torch.log(probs), dim=1)
    avg_loss = torch.mean(train_loss)
    return avg_loss
In [43]:
manual_cross_entropy(logits, y)
Out[43]:
tensor(0.4555)

4. Using PyTorch's CrossEntropyLoss¶

  • we don't need to apply softmax activation
  • we don't need to convert true labels to one-hot encoding
In [44]:
import torch
import torch.nn.functional as F
In [45]:
# We have 4 samples and 3 classes
# "logits" is the output of the model before applying softmax
logits = torch.tensor([
    [1.5, 0.1, -0.4],
    [0.5, 0.7, 2.1],
    [-2.1, 1.1, 0.8],
    [1.1, 2.5, -1.2]
])
In [46]:
y = torch.tensor([0, 2, 2, 1])
y_onehot = F.one_hot(y, num_classes=3)
print(y_onehot)

tensor([[1, 0, 0],
        [0, 0, 1],
        [0, 0, 1],
        [0, 1, 0]])
In [47]:
loss = F.cross_entropy(logits, y)
loss
Out[47]:
tensor(0.4555)